Estrategias básicas en programación. Ejemplo: búsqueda de soluciones a problema con iteración (CU00111A)

 

 

Objetivo: Buscar el valor de x que siendo un número real positivo hace f(x) = 5x² - 3x - 4 igual a cero de acuerdo con estas reglas.

 

1.   Se admite la desviación de f(x) respecto al valor pedido de ± 0'01.

2.   Hemos perdido toda nuestra memoria: no se admite el uso de fórmulas o estrategias de resolución gráficas o analíticas: debemos basarnos en un tanteo puro ordenado (no aleatorio) y constante.

3.   Se sabe que la solución está entre 1 y 10, debiendo comenzar la búsqueda por uno de estos dos extremos.

 

Se pide: definir el esquema de búsqueda limitando el número máximo de iteraciones.

 

 

 

Primer paso: reflexionar sobre el problema. Muy rápidamente podemos plantear:

Vayamos a todo lo que son datos para resolver el problema. Para acostumbrarnos a resolver problemas genéricos, es decir, con variables no fijadas, usaremos letras en vez de números.

 

Datos:

 

·       f(x) = ax² + bx + c , función.

·       e , error admisible.

·       lim inf , límite inferior del intervalo de búsqueda.

·       lim sup , límite superior del intervalo de búsqueda.

·       int , valor incremental para cada tanteo.

·       Nmax , número máximo de iteraciones.

 

Los únicos datos que nos faltan son los de incrementos en cada tanteo y número máximo de iteraciones. Podríamos hacer muchas cosas, pero nuestro planteamiento inicial va a ser el siguiente:

 

·       Trataremos de barrer todo el intervalo de búsqueda.

·       En nuestro caso el intervalo de búsqueda comprende 10 – 1 = 9 enteros.

                 

 

sería el intervalo para realizar 10000 tanteos. Vamos a redondear a 0,001 con lo cual

 

 

 ·       Cerraremos el asunto estableciendo: int = ± 0,001 ; N_max = 9000

 

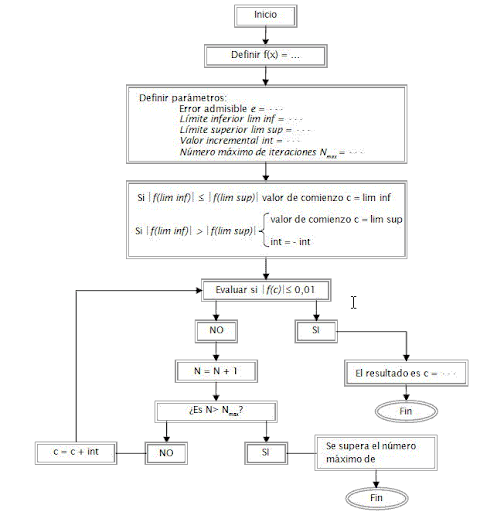
Pasemos ahora al procedimiento. En primer lugar, ¿Qué extremo del intervalo elegir? Optaremos por evaluar las funciones en ambos puntos, y empezaremos por aquel punto cuya imagen sea más próxima a cero. Es decir, si |f(lim inf)| < |f(lim sup)| entonces se comienza por límite inferior y en caso contrario por límite superior. Evaluaremos la imagen del punto inicial y si resulta inferior o igual al valor admisible e, daremos por resuelto el problema. En caso contrario, evaluaremos si hemos llegado al número máximo de iteraciones, y si no es así, volveremos a repetir el proceso para un valor a evaluar igual al anterior más el intervalo de búsqueda. Por último haremos este esquema reflejo de todo lo anterior.